Productiekosten

Een onderneming maakt kosten die onafhankelijk zijn van de hoeveelheid produkt die wordt gemaakt en die daarom constante of vaste kosten worden genoemd. Voorbeelden: de kosten van de fabriekshal en de machines. Daarnaast zijn er de variabele kosten die wel veranderen naarmate er meer of minder wordt geproduceerd. Voorbeelden: grondstoffen, energie. In de tabel is een eenvoudig getallenvoorbeeld gekozen om de samenhang van een aantal kostenbegrippen te laten zien. In de eerste kolom staat het aantal stuks produkt, lopend van 0 tot en met 10.

In de tweede kolom zijn de totale constante kosten gegeven. We zien dat deze bij elke productie 5 bedragen. In kolom 3 staan de totale variabele kosten. De totale kosten (kolom 4) vinden we door steeds de TCK (kolom 2) en de TVK (kolom 3) bij elkaar te tellen, ofwel TK = TCK + TVK.

De totale kosten blijken te stijgen als er meer wordt geproduceerd. Dat hoeft ons niet te verbazen: naarmate er meer producten worden gemaakt worden er, bovenop het bedrag aan constante kosten meer variabele kosten gemaakt.

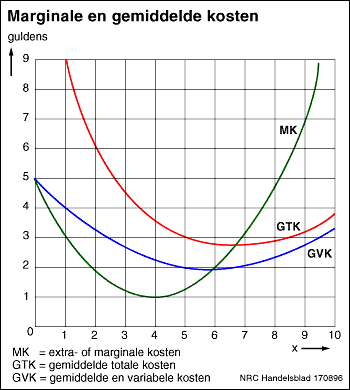
Totale, marginale en gemiddelde kosten

[bij tabel: let op dat marg.kosten steeds TUSSEN twee waarden van totale kosten staat]

Aantal stuks x	Totale constante kosten TCK	Totale variabele kosten TVK	Totale kosten TK	Extra- of marginale kosten MK	Gemiddelde totale kosten GTK	Gemiddelde variabele kosten GVK
0	5	0,0	5,0	4,0	-	5,0
1	5	4,0	9,0	2,7	9,0	4 ,0
2	5	6,7	11,7	1,6	6,0	3,3
3	5	8,3	13,3	1,0	4,4	2,8
4	5	9,3	14,3	1,1	3,6	2,3
5	5	10,4	15,4	1,6	3,1	2,0
6	5	12,0	17,0	2,6	2,8	2,0
7	5	14,6	19,6	3,9	2,8	2,1
8	5	18,5	23,5	5,7	2,9	2,3
9	5	24,2	29,2	8,8	3,2	2,7
10	5	33,0	38,0		3,8	3,3

De kolom marginale kosten heeft de volgende betekenis. Voor een producent is het interessant om te weten wat zijn totale kosten bij elke productie-omvang zijn. Maar daarnaast wil hij ook graag weten wat het hem extra kost als hij zijn productie met één eenheid uitbreidt. Deze extra kosten of marginale kosten (MK) heeft hij nodig om te kunnen bepalen hoeveel hij moet verkopen om zijn winst zo groot mogelijk te maken. We komen daar nog op terug.

Nu gaan we na hoe je de marginale kosten kunt uitrekenen aan de hand van de totale kosten. In de tabel zijn de totale kosten bij een productie van bijvoorbeeld 2 stuks gelijk aan 11,7 en bij 3 stuks zijn ze 13,3. De extra- of marginale kosten van het produceren van 3 in plaats van 2 stuks zijn dus 13,3 - 11,7 = 1,6. Nog een voorbeeld: de marginale kosten van de 8ste eenheid produkt zijn gelijk aan 23,5 - 19,6 = 3,9.

In de tabel staan de marginale kosten in de vijfde kolom. In de figuur zijn ze getekend. We zien dat ze zowel in de tabel als in de figuur steeds precies tussen twee op elkaar volgende produktiehoeveelheden staan. De marginale kostenkromme daalt eerst, bereikt een dieptepunt en stijgt vervolgens: hij heeft een U-vormig verloop. We gaan er hier niet op in waarom dit zo is.

Het is voor een ondernemer ook belangrijk dat hij de kostprijs van zijn produkt kent. Dit zijn de totale kosten per stuk ofwel de gemiddelde totale kosten (GTK). Die heeft hij nodig om te kunnen bepalen welke verkoopprijs hij voor zijn produkt zal vragen. Die verkoopprijs is gelijk aan de kostprijs plus een bepaalde winstopslag.
De GTK bij een bepaalde productie-omvang worden gevonden door de totale kosten te delen door die productie-omvang. Voorbeeld: de TK bij 3 stuks zijn 13,3; daaruit volgt voor de totale kosten per stuk: TK/x = 13,3 : 3 = 4,4. In de tabel staan de GTK in de zesde kolom. In de figuur blijkt dat ze evenals de marginale kosten een U-vormig verloop hebben.

Soms wil een ondernemer ook graag weten wat per stuk de variabele kosten zijn. Deze gemiddelde variabele kosten (GVK) worden gevonden als TVK/x.Ze staan in de zevende kolom van de tabel en in de figuur blijken ook de GVK een U-vormig verloop te hebben.

Figuur Marginale en gemiddelde kosten